2D Ising model with competing orders
$$ S=K\sum_{\langle i,j\rangle} s_i s_j + V \sum_{\langle \langle i,j\rangle\rangle} s_i s_j $$
green bonds are nearest couplings \(\langle i,j\rangle\); the red bonds are next nearest couplings \(\langle\langle i,j\rangle\rangle\)
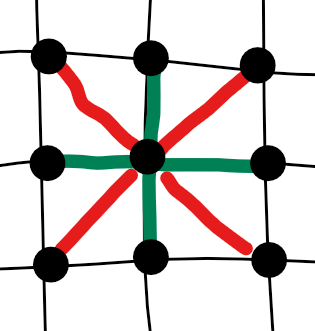
the system gets very rich phase diagram, for example, when
physics experiments you can do!
1. explore the phases
when \(K=0\), the system can be divided into two decoupled sub-systems.
\(V=-\infty\) gives two anti-ferromagnetic system, according to their relative postition, we can have either vertial strip order or horizantal strip order.
2. hysteresis effect
- tune \(V\) to the largest postive value
- tune \(K\) to zero.
- set updating speed to maximum
- wait some time, until domain wall disappear
- now tune \(K\) slowly from 0 to 0.2
- and then tune \(K\) slowly from 0.2 to -0.2
- go back tune \(K\) slowly from -0.2 to 0.2
- you will see a hysteresis effect happen near \(K=\pm 0.14\), for \(V=1\)
3. neutron scattering
I will add FFT feature later, where you can see the scattering plot.
